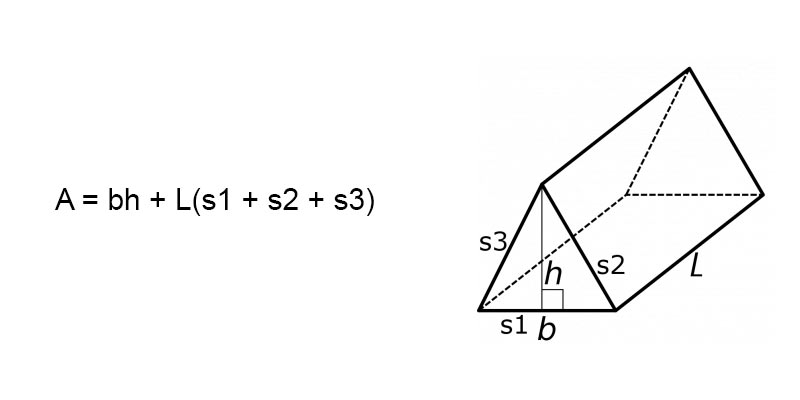
If it is a rectangular shape, it is called a quadrangular prism. If it has a triangular shape, it is a triangular prism. In the prism, there are various three-dimensional shapes.
SURFACE AREA OF A PRISM HOW TO
To understand how to find the surface area, we must understand the types of prisms and cylinders.
There are two main types of pillar shapes: prisms and cylinders.
Two Types of Pillar Shapes: Prismatic and Cylindrical
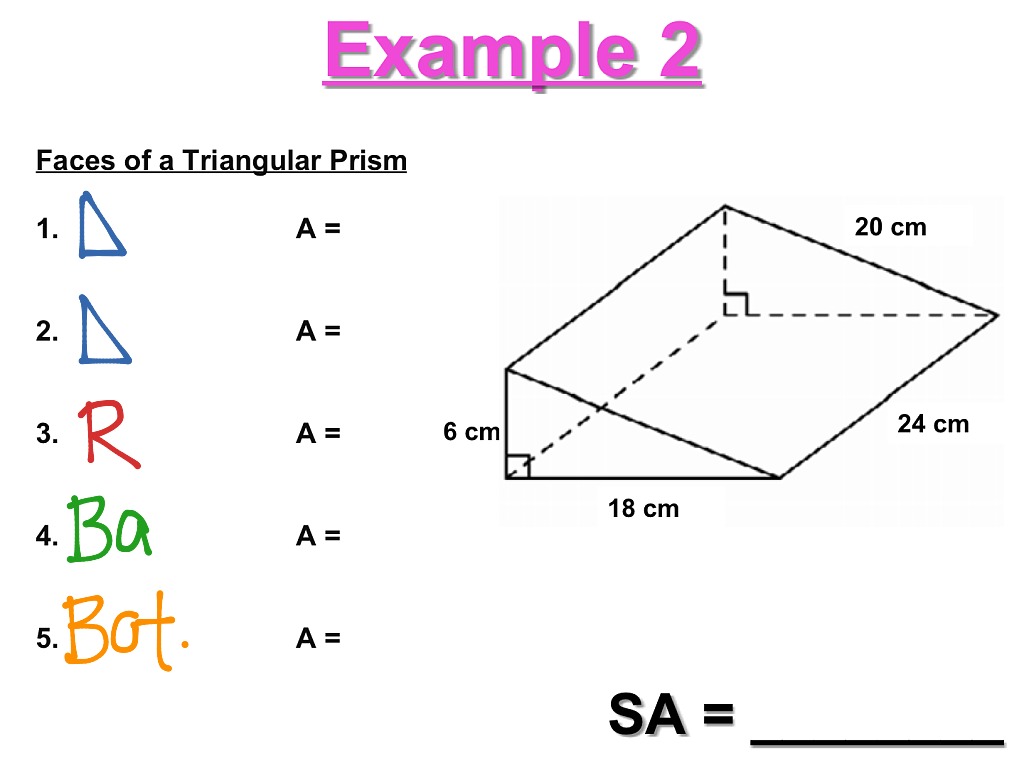4 Calculating the Surface Area of Prisms and Cylinders. 3 Exercises: Surface Area of Prisms and Donuts Shapes (Hollow Cylinders). 2.2 Calculating Surface Area from a Cylinder Net. 2.1 How to Calculate the Surface Area of a Prism. 2 The Total Area of the Net Is the Surface Area. 1.1 Adding Base Areas and Side Area Yields the Surface Area. 1 Two Types of Pillar Shapes: Prismatic and Cylindrical. The total surface area formula for a hexagonal prism is given as:Ĭalculate the total surface area of an isosceles trapezoid whose parallel sides of the base are 50 mm and 120 mm and legs of the base are 45 mm each, the height of the base is 40 mm, and the height of the prism is 150 mm. Thus, the cost of painting the rectangular prism is $3,600įind the total surface area of a hexagonal prism whose apothem length, base length, and height are given as 7 m, 11 m, and 16 m, respectively. The total cost of painting the prism = TSA x cost of painting Surface area of a rectangular prism = 2h (l +b) If the painting cost is $50 per square inch, find the total cost of painting all faces of the prism.įirst, calculate the total surface area of the prism Thus, the total surface area of the pentagonal prism is 1885 cm 2Ī rectangular prism of dimensions, length = 7 in, width = 5 in and height = 3 in is to be painted. The formula for the total surface area of a pentagonal prism is given by Find the total surface area of the pentagonal prism. The apothem length, base length, and height of a pentagonal prism are 10 cm. Hence, the total surface area of the prism is 343.44 cm 2. Thus, the apothem length of the prism is 6.93 cm The base is an equilateral triangle of side 8 cm.īy Pythagorean theorem, the apothem length, a of the prism is calculated as: Therefore, the total surface area of the triangular prism is 240 cm 2.įind the total surface area of a prism whose base is an equilateral triangle of side 8 cm and height of the prism is 12 cm. Now substitute the base area, height, and perimeter in the formula. Since the base is a triangle, then the base area, B =1/2 ba TSA = 2 x area of the base + perimeter of the base x Height The other two sides of the triangular base are 7 cm each.įind the total surface area of the triangular prism. The dimensions of a triangular prism are given as follows: Let’s solve a few example problems involving the surface area of different types of prisms. Note: The formula to find the base area (B) of a prism depends on the base’s shape. Where TSA = Total surface area of a prism Total surface area of a prism = 2 x area of the base + perimeter of the base x Height Therefore, the surface area of a prism formula is given as: Since we know the total surface area of a prism is equal to the sum of all its faces, i.e., the floor, walls, and roof of a prism. Add up the area of the two bases and the area of the lateral faces to get the total surface area of a prism. And then calculate the area of lateral faces connecting the bases. To find the total surface area of a prism, you need to calculate the area of two polygonal bases, i.e., the top face and bottom face. In a prism, the lateral faces, which are parallelograms, are perpendicular to the polygonal bases. A prism is named according to the shape of the polygonal bases. To recall, a prism is a 3-dimensional polyhedron with two parallel and congruent bases, which are connected by lateral faces. In this article, you will learn how to find the total surface area of a prism by using the surface area of a prism formula. The total surface area of a prism is the sum of areas of its lateral faces and its two bases. Surface Area of a Prism – Explanation & Examples
0 kommentar(er)
